> 재귀함수
n=3일 경우
1번 초기값을 제외한 7번의 과정을 통해
하노이 탑을 수행한다.
기둥은 총 3개
f , m , e 순서로 나열되어 있다.
우리는 f 에 있는 원판을 e로 옮겨야한다.
여기서 신경써야 할 조건은
작은 원판이 큰 원판 아래에 있을 수 없다는 것.
이동 횟수가 최소가 되어야 한다는 점.
아래 그림처럼
하나하나 조건을 다 나눠줘야하나 생각했다.
왜 알고리즘 문제를 풀때마다
세부적으로 세세하게 생각을 하는지 ㅠㅠ
큰 틀을 바라봐보기 위해 노력하였다.
그랬더니
맨 아래에 있는 가장 크기가 큰 원판을 제외한 나머지 원판이
m 위치의 기둥에 있어야 하고
f 기둥에 남아있는 원판이
e 기둥으로 옮겨져야 한다.
마지막으로 m 기둥에 있는 원판이 e 기둥으로 옮겨지면 끝!
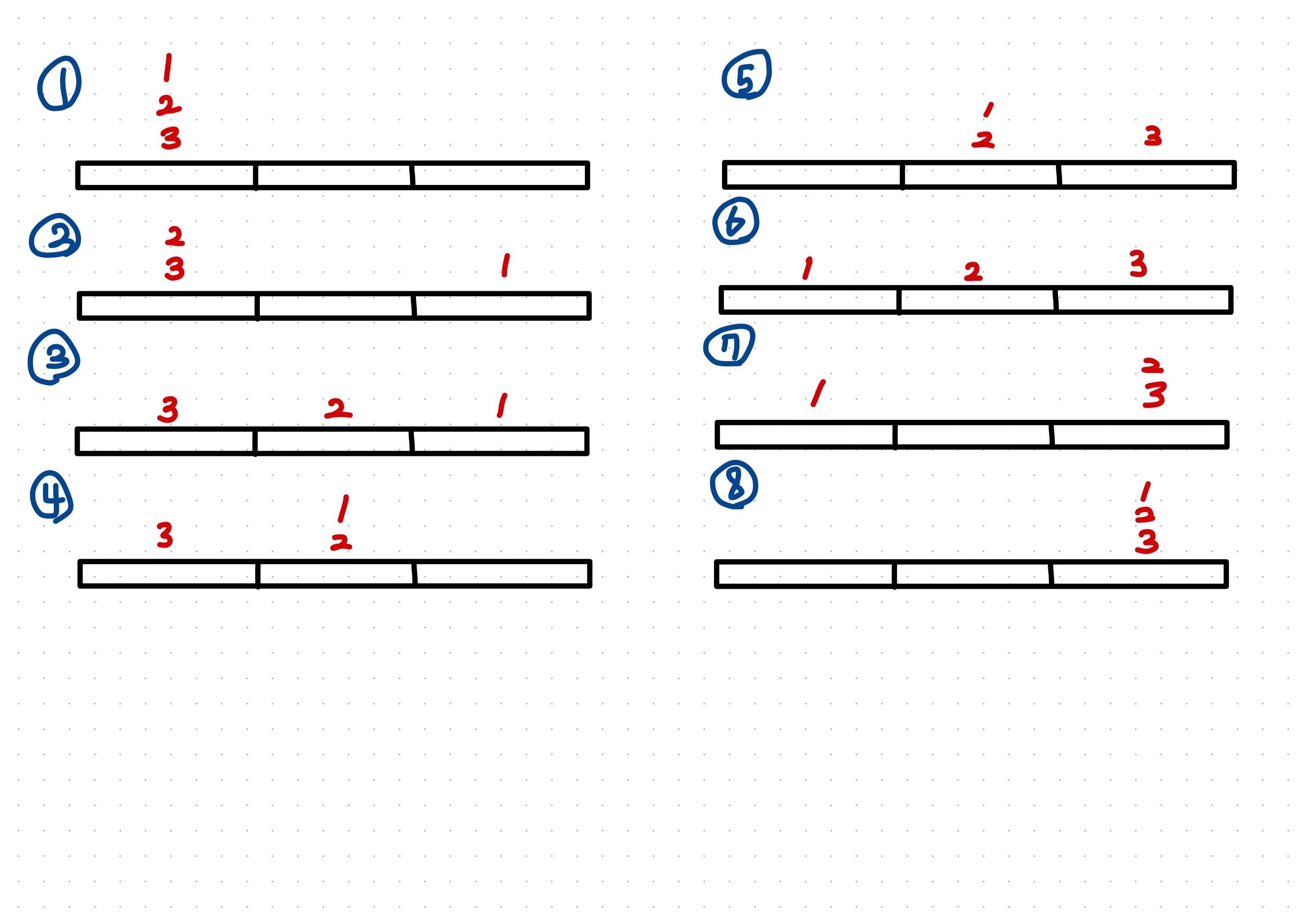
n=3
hanoi(3,1,3,2) # 3개의 원판을 1번 기둥 -> 3번 기둥으로 이동, 2번 기둥은 보조 기둥
hanoi(2,1,2,3) # 2개의 원판을 1번 기둥 -> 2번 기둥으로 이동, 3번 기둥은 보조기둥
hanoi(1,1,3,2) ## 1개의 원판을 1번 기둥 -> 3번 기둥으로 이동, 2번 기둥은 보조기둥
print(1,3)
print(1,2) ## 2개의 원판 중 가장 큰 원판을 1번 기둥 -> 2번 기둥으로 이동
hanoi(1,3,2,1) ## 1개의 원판을 3번 기둥 -> 2번 기둥으로 이동, 1번 기둥은 보조기둥
print(3,2)
print(1,3) # 가장 큰 원판을 1번 기둥 -> 3번 기둥으로 이동
hanoi(2,2,3,1) # 2개의 원판(2번에 남아 있던) -> 3번 기둥으로 이동, 1번 기둥은 보조기둥
hanoi(1,2,1,3) ## 1개의 원판을 2번 기둥 -> 1번 기둥으로 이동
print(2,1)
print(2,3) ## 2개의 원판 중 가장 큰 원판을 2번 기둥 -> 3번 기둥으로 이동
hanoi(1,1,3,2) ## 1개의 원판을 1번 기둥 -> 3번 기둥으로 이동
print(1,3)아래 코드의 과정을 풀어쓰면
위와 같다.
넘 헷갈렸다 ㅠㅠ
** 일단 하노이탑 알고리즘을 정리해보기 **
1. 1번 기둥(f)에 있는 n-1개의 원판이 보조기둥인 2번 기둥(t)로 이동
2. 1번 기둥(f)에 에 남아있는 가장 큰 원판을 3번 기둥(e)으로 이동
3. 보조기둥인 2번 기둥(t)에 있는 n-1개의 원판을 3번 기둥(e)로 이동
n = int(input())
def hanoi(n, f, e, m):
if n == 1:
print(f, e)
return
hanoi(n - 1, f, m, e) # f 기둥 -> m 기둥 , e 기둥은 보조기둥
print(f, e)
hanoi(n - 1, m, e, f) # m 기둥 -> e 기둥, f 기둥은 보조기둥
if n <= 20:
# 과정 출력
print(pow(2, n) - 1)
hanoi(n, 1, 3, 2)
else:
# 과정 출력 x
print(pow(2, n))'여니의 취준 준비 > 코딩테스트 (Python)' 카테고리의 다른 글
| [9084] 동전 In python (0) | 2022.02.20 |
|---|---|
| [14891] 톱니바퀴 in python (0) | 2022.02.20 |
| [2346] 풍선 터뜨리기 in python (0) | 2022.02.16 |
| [15961] 회전 초밥 in python (0) | 2022.02.13 |
| [2688] 줄어들지 않아 In python (0) | 2022.02.13 |
